上一篇
机器学习🔍混淆矩阵详解:核心机制解析与实战操作全攻略
- 问答
- 2025-08-08 13:56:53
- 7
本文目录导读:
🎉 机器学习🔍混淆矩阵详解:核心机制解析与实战操作全攻略 🎉
📊 混淆矩阵核心机制解析
混淆矩阵是分类模型的“体检报告”,用表格形式直观展示预测结果与真实标签的对应关系,以二分类为例,矩阵包含四个关键指标:
| 实际\预测 | 正类(Positive) | 负类(Negative) |
|---|---|---|
| 正类(Positive) | ✅ TP(真正例) | ❌ FN(假负例) |
| 负类(Negative) | ❌ FP(假正例) | ✅ TN(真负例) |
- TP(True Positive):模型正确预测为正类的样本数(如正确识别垃圾邮件)。
- TN(True Negative):模型正确预测为负类的样本数(如正确放过非垃圾邮件)。
- FP(False Positive):模型误将负类预测为正类(如误判正常邮件为垃圾邮件,误报!)。
- FN(False Negative):模型漏掉正类样本(如漏判垃圾邮件,漏报!)。
🔍 核心指标计算
通过混淆矩阵可衍生出多个评估指标,帮你精准定位模型优缺点:
| 指标 | 公式 | 意义 |
|---|---|---|
| 准确率(Accuracy) | ( \frac{TP + TN}{TP + TN + FP + FN} ) | 整体预测正确率,但可能掩盖类别不均衡问题(如99%负类样本时,全猜负类准确率99%但无意义)。 |
| 精确率(Precision) | ( \frac{TP}{TP + FP} ) | 预测为正类的样本中,真正例的比例(降低误报,如“标记为垃圾邮件的邮件中,确实是垃圾邮件的比例”)。 |
| 召回率(Recall) | ( \frac{TP}{TP + FN} ) | 实际正类中被正确预测的比例(降低漏报,如“所有垃圾邮件中被正确拦截的比例”)。 |
| F1值(F1-Score) | ( \frac{2 \times Precision \times Recall}{Precision + Recall} ) | 精确率与召回率的调和平均,平衡误报与漏报(如医疗诊断中需同时控制假阳性和假阴性)。 |
🚀 实战操作全攻略
步骤1:生成混淆矩阵
使用Python的sklearn库一键生成:
from sklearn.metrics import confusion_matrix y_true = [1, 0, 1, 1, 0] # 真实标签 y_pred = [1, 1, 1, 0, 0] # 预测标签 cm = confusion_matrix(y_true, y_pred) print(cm) # 输出:[[1 1], [1 2]](TN=1, FP=1, FN=1, TP=2)
步骤2:可视化分析
用热力图让矩阵“活”起来:
import seaborn as sns
import matplotlib.pyplot as plt
sns.heatmap(cm, annot=True, fmt="d", cmap="Blues",
xticklabels=["Negative", "Positive"],
yticklabels=["Negative", "Positive"])
plt.xlabel("Predicted")
plt.ylabel("Actual")"Confusion Matrix 🔍")
plt.show()
步骤3:优化模型
- 调整分类阈值:通过调整模型输出概率的阈值,平衡精确率与召回率(如降低阈值可提高召回率但可能增加误报)。
- 处理类别不均衡:对少数类样本过采样(如SMOTE算法)或调整损失函数权重。
🌰 实战案例:医疗诊断
假设模型用于癌症筛查:
- TP:正确识别癌症患者(及时治疗)。
- FP:误判健康人为癌症(导致不必要的焦虑)。
- FN:漏诊癌症患者(延误治疗,后果严重!)。
- TN:正确排除健康人。
此时应优先提高召回率(减少FN),即使牺牲部分精确率(允许更多FP),因为漏诊的代价远高于误诊。
💡 进阶技巧
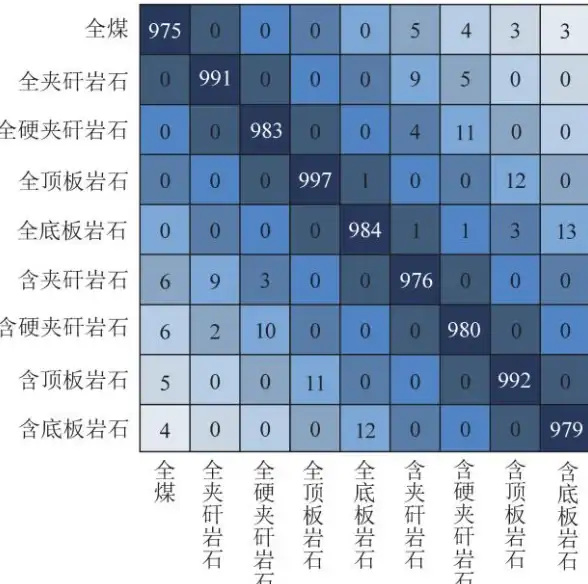
- 多分类混淆矩阵:扩展为n×n矩阵,分析模型在各类别上的混淆情况(如将“猫”误判为“狗”或“汽车”)。
- 结合ROC曲线:通过混淆矩阵计算真正率(TPR=Recall)和假正率(FPR=FP/(FP+TN)),绘制ROC曲线评估模型在不同阈值下的性能。
📚 参考资料(2025-08更新)
- CSDN博客《机器学习模型的评估:混淆矩阵》
- 腾讯云《机器学习 - 混淆矩阵:技术与实战全方位解析》
- 阿里云开发者社区《数据分析必学技能:混淆矩阵原理详解,Python调用实战》
通过混淆矩阵,你不仅能知道模型“对不对”,还能知道它“哪里不对”,从而针对性优化!快去实战中试试吧~ 🚀
本文由 业务大全 于2025-08-08发表在【云服务器提供商】,文中图片由(业务大全)上传,本平台仅提供信息存储服务;作者观点、意见不代表本站立场,如有侵权,请联系我们删除;若有图片侵权,请您准备原始证明材料和公证书后联系我方删除!
本文链接:https://up.7tqx.com/wenda/568679.html






发表评论